Télécharger

Vote des utilisateurs

Voir les 4 commentaires

Détails

Jérôme Briot

Rédacteur / Modérateur

52958 points

Voir tous les téléchargements de l'auteur

Licence : Libre

Mise en ligne le 4 juin 2014

Plate-formes : Linux, Mac, Windows

Langue : Français

Référencé dans

Fractales

Navigation

Retourner à la liste des ressources Retourner à l'accueil des téléchargements Ajouter un LOGICIELAjouter un FRAMEWORKAjouter un CODE SOURCE

Jeu du chaos - Chaos Game (2D/3D)

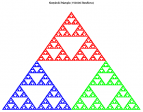
Voici un ensemble de codes MATLAB permettant de générer et d'afficher des fractales via le jeu du chaos (chaos game) à partir d'une grammaire donnée et pour N itération

Le code MATLAB principal prend en entrée une structure form est une structure avec les champs suivant

form.name
form.polyg
form.frac
form.keeppolyg

En prenant l'exemple du Triangle de Sierpinski (voir http://en.wikipedia.org/wiki/Sierpinski_triangle#Construction et le paragraphe qui commence par "Or more simply:"), la structure form est :

form.name = 'Sierpinski triangle';
form.polyg = [0 1 .5 ; 0 0 sqrt(2)/2];
form.frac = .5;
form.keeppolyg = true;

Le champs keeppolyg sert juste à spécifier si les points du polygone de départ doivent être conservés ou non pour le tracé final.

Signaler un problème

Jerome Briot

Rédacteur/Modérateur

Le 03/09/2009 à 19:02

Quelques images...

Jerome Briot

Rédacteur/Modérateur

Le 03/09/2009 à 19:03

Sources

A compléter...

Jerome Briot

Rédacteur/Modérateur

Le 03/09/2009 à 22:14

Quelques formes en plus tiré du site Wolfram Mathworld

Fonction SELECTCHAOSGAMEFORM mise à jour dans le premier message

Jerome Briot

Rédacteur/Modérateur

Le 04/09/2009 à 10:18

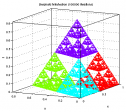
Voici la version 3D :

Code :

Sélectionner tout

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
function chaosgame3d(form,N)
%CHAOSGAME3D
%
%

% Author : Jerome Briot (Dut)
% Contact : dutmatlab#yahoo#fr -or- briot#cict#fr
% Profil : www.mathworks.com/matlabcentral/newsreader/author/94805
%        : www.developpez.net/forums/u125006/dut/
%
% Version : 1.0 - 03 Sep 2009
%

% MATLAB : 7.6.0.324 (R2008a)
% System : Linux 2.6.24-24-generic
%

if nargin==0

    form.name = 'Sierpinski tetrahedron';
    form.polyg = [0 1 .5 .5 ; 0 0 sqrt(3)/2 sqrt(3)/6 ; 0 0 0 sqrt(2/3)];
    form.frac = .5;
    form.keeppolyg = true;

    N = 100000;
    
end

xs = .5+rand/10;
ys = .5+rand/10;
zs = .5+rand/10;

sp = size(form.polyg,2);

idx = randperm(sp);


x = zeros(1,N);
y = zeros(1,N);
z = zeros(1,N);
c = zeros(1,N);

if form.keeppolyg
    x(1:sp) = form.polyg(1,:);
    y(1:sp) = form.polyg(2,:);
    z(1:sp) = form.polyg(3,:);
    c(1:sp) = 1:sp;
    k = sp+1;
else
    k = 1;
end

x(k) = form.frac*form.polyg(1,idx(1))+(1-form.frac)*xs;
y(k) = form.frac*form.polyg(2,idx(1))+(1-form.frac)*ys;
z(k) = form.frac*form.polyg(3,idx(1))+(1-form.frac)*zs;
c(k) = idx(1);

for n=k+1:N
    idx = randperm(sp);
    x(n) = form.frac*form.polyg(1,idx(1))+(1-form.frac)*x(n-1);
    y(n) = form.frac*form.polyg(2,idx(1))+(1-form.frac)*y(n-1);
    z(n) = form.frac*form.polyg(3,idx(1))+(1-form.frac)*z(n-1);
    c(n) = idx(1);
end

figure('color','w')

mc = max(c);

hold on
cmap = hsv(mc);
cmap = cmap(randperm(mc),:);

for n = 1:mc
    idx = c==n;
    h(n) = plot3(x(idx),y(idx),z(idx),'k.');
    set(h(n),'color',cmap(n,:));
end
title(sprintf('%s (%d iterations)',form.name,N))
view(3);
xlabel('x');
ylabel('y');
zlabel('z');
box on
grid on
axis equal on vis3d

Rien de bien compliqué a priori puisqu'il suffit juste d'ajouter une dimension supplémentaire au problème (aucun soucis, qui l'eut cru

)

Poster un commentaire

Developpez.com décline toute responsabilité quant à l'utilisation des différents éléments téléchargés.