En utilisant la fonction stairsDocumentation de la fonction stairs

Exemple :

X = [0 1 0 1 1 0 0 0 1 1 1 1 0 1 0 1 0];

figure
stairs(X)
axis equal

Les filtres sont représentés dans le domaine complexe de z par la fonction de transfert suivante :

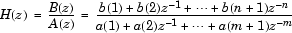
donc pour définir un filtre, il faut connaître les coefficients du numérateur et du dénominateur. Sous MATLAB, ces coefficients doivent être rangés dans deux vecteurs lignes a et b, puis, pour effectuer le filtrage, il suffit de taper :

y = filter(b,a,x);

Remarque : le coefficient a(1) ne doit jamais être nul.

Plusieurs fonctions MATLAB permettent de réaliser des filtres classiques et simples, nous en citerons quelques unes : fir1Documentation de la fonction fir1, fir2Documentation de la fonction fir2, firlsDocumentation de la fonction firls, firpmDocumentation de la fonction firpm, butterDocumentation de la fonction butter…

La plus simple est la fonction fir1 qui permet de réaliser un filtre FIR. Elle génère les coefficients b seulement (donc a=1). Il suffit de choisir l'ordre n du filtre et les fréquences de coupures normalisées rangées dans un vecteur W_n dans l'ordre croissant. Puisque les fréquences sont normalisées, alors W_n contient des éléments entre 0 et 1, 0 pour la fréquence zéro, et 1 pour représenter la fréquence de Nyquist (la moitié de la fréquence d'échantillonnage).

Exemple :

Pour réaliser un filtre passe bande [200 400] kHz et d'ordre 4 avec la fréquence d'échantillonnage fs=1000 kHz :

fs = 1e6;
Wn = 2*[2e5 4e5]/fs;
b = fir1(4,Wn);
freqz(b,1);

La fonction fir1 peut admettre un troisième paramètre pour préciser le type de filtre :

b = fir1(n,Xn,ftype);

avec ftype qui peut prendre :

• 'high' pour un filtre passe haut ;
• 'stop' pour un filtre coupe bande ;
• 'DC-1' pour faire du premier interval un passe bande, dans le cas d'un multibande ;
• 'DC-0' pour faire du premier interval un coupe bande, dans le cas d'un multibande.

Pour déterminer l'enveloppe d'un signal, il suffit d'utiliser la fonction hilbertDocumentation de la fonction hilbert de la Signal Processing Toolbox.

Lorsque la fonction hilbert est appliquée à un signal x, elle renvoie un vecteur complexe y (généralement appelé signal analytique) de même taille que x, dont la partie réelle est exactement x et la partie imaginaire est la transformée d'Hilbert du signal x.

L'enveloppe du signal x est tout simplement le module de y.

y = hilbert(x);
env = abs(y);

La transformée de Fourier d'un signal pair donne un signal réel, et la définition d'un signal pair est telle que x(-t)=x(t). Or avec MATLAB, on suppose toujours que le premier élément d'un vecteur est l'origine (t=0), donc le signal est décalé.

Puisque le décalage d'un signal influe directement sur sa phase, on comprend bien pourquoi on ne trouve pas une fft réelle pour un signal pair.

Pour compenser l'erreur introduite par le décalage, on divise le résultat obtenu par le déphasage correspondant au décalage.

Exemple :

x = [1:9 10 9:-1:1];
X = fft(x,1024);
k = 0:1023;
dephasage = exp(-j*2*pi*k*9/1024);
X = real(X./dephasage);

Pour trouver les coefficients a et b d'un filtre IIR en ayant sa réponse impulsionnelle, il suffit d'utiliser la fonction pronyDocumentation de la fonction prony de la Signal Processing Toolbox, et de décider de l'ordre du numérateur n et du dénominateur m :

[b, a] = prony(h,n,m);

En géneral, la longueur du vecteur h est supérieure à m et n. Si ce n'est pas le cas, h est completé par des zéros.

Pour transformer un signal sous forme d'une chaîne de caractères composée de 0 et de 1 en vecteur numérique, il faut simplement lui soustraire la valeur 48 comme ceci :

>> X = '01011000111101010'

X =

01011000111101010

>> X = X-48

X =

     0     1     0     1     1     0     0     0     1     1     1     1     0     1     0     1     0

En effet 48 est la valeur du caractère '0' dans la table ASCII. Donc '0'-48 donne 0 et '1'-48 donne 1.