Il existe plusieurs cas de calcul d'intégrale :

• connaissant l'expression d'une fonction, on cherche à obtenir l'expression d'une primitive. Ce calcul sous MATLAB nécessitera la Symbolic Math Toolbox et se fera avec la fonction intDocumentation de la fonciton int :

   

  Sélectionnez

  >> syms x z
  >> int(x/(1 + z^2), x) % Selon la variable x
   
  ans =
   
  x^2/(2*(z^2 + 1))
   
  >> int(x/(1 + z^2), z) % Selon la variable z
   
  ans =
   
  x*atan(z)

• connaissant l'expression d'une fonction, on cherche à obtenir son intégrale entre deux bornes. On utilisera pour cela la fonction quadDocumentation de la fonction quad (ou integralDocumentation de la fonction integral depuis la version 2012a).

   

  Sélectionnez

  >> fun = @(x) x.^2;
  >> integral(fun, 0, 1)
  
  ans =
  
      0.3333
  
  >> quad(fun, 0, 1)
  
  ans =
  
      0.3333

  Voir le 1) et 2) du sujet Que représente le symbole @ ? expliquant la syntaxe utilisée pour la fonction en premier paramètre.

  Le calcul d'intégrales doubles et triples pourra se faire de la même façon avec les fonctions dblquadDocumentation de la fonction dblquad et triplequadDocumentation de la fonction triplequad (ou integral2Documentation de la fonction integral2 et integral3Documentation de la fonction integral3 depuis la version 2012a).

  La fonction int précédente de la Symbolic Math Toolbox peut aussi effectuer ce calcul de manière symbolique :

   

  Sélectionnez

  >> syms x
  >> int(x.^2, 0, 1)
   
  ans =
   
  1/3

• possédant un tableau de valeurs représentant une courbe, on cherche à calculer son intégrale, ou aire, on utilisera alors la fonction trapzDocumentation de la fonction trapz :

   

  Sélectionnez

  >> x = linspace(0, 1, 1000);
  >> y = x.^2;
  >> trapz(x,y)
  
  ans =
  
      0.3333

Il existe plusieurs cas de calcul de dérivée :

• connaissant l'expression d'une fonction, on cherche à obtenir l'expression de sa dérivée. Ce calcul sous MATLAB nécessitera la Symbolic Math Toolbox et se fera avec la fonction diffDocumentation de la fonction diff :

   

  Sélectionnez

  >> syms t x
  >> diff(x*sin(t^2), t) % Dérivée selon la variable t
  
  ans =
   
  2*t*x*cos(t^2)
  
  >> diff(t^6, t, 3) % Dérivée troisième selon la variable t
   
  ans =
   
  120*t^3

• possédant un tableau de valeurs représentant une courbe, on cherche à obtenir les valeurs de la dérivée. On utilisera alors la fonction MATLAB diffDocumentation de la fonction diff de base :

   

  Sélectionnez

  t = 0:0.01:2*pi;
  y = sin(t);
  dy = diff(y) ./ diff(t);

  Note : dans le cas d'un écart constant entre les échantillons, on peut remplacer le terme diff(t) par cet écart. Par exemple ici dy = diff(y) / 0.01;.

• connaissant l'expression d'une fonction, on cherche à obtenir la valeur de la dérivée en un certain point. On pourra réutiliser le premier point sur lequel on appliquera la fonction subsDocumentation de la fonction subs :

   

  Sélectionnez

  syms t
  derivee = diff(t^6, t);
  subs(derivee, t, 1)

  Ou appliquer la formule de la dérivée 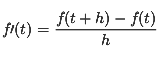avec h suffisamment petit.

L'ajustement de courbe revient à estimer les paramètres d'un modèle théorique donné à partir de données expérimentales. Cette estimation s'effectue par la méthode des moindres carrés à l'aide de différentes fonctions MATLAB selon la nature du modèle :

Modèle linéaire

• opérateur \Documentation de l'opérateur \ (fonction mldivide) on pourra consulter le minitutoriel Ajustement aux moindres carrés de courbes et de surfaces pour plus de précisions.

Les fonctions qui suivent nécessitent l'Optimization Toolbox.

Modèle linéaire, avec une contrainte de valeurs positives

• lsqnonnegDocumentation de la fonction lsqnonneg

Modèle linéaire avec contrainte

• lsqlinDocumentation de la fonction lsqlin

Modèle non-linéaire

• lsqcurvefitDocumentation de la fonction lsqcurvefit
• lsqnonlinDocumentation de la fonction lsqnonlin

Afin d'approximer une courbe par un polynôme, on pourra utiliser la fonction polyfitDocumentation de la fonction polyfit.

Pour effectuer une interpolation, il est d'abord nécessaire d'avoir une série d'éléments de référence de l'espace de départ pour laquelle les éléments correspondants de l'espace d'arrivée sont connus. Le but de l'interpolation est alors de se servir de ces données existantes afin de calculer de nouveaux éléments de correspondance suivant au mieux ce modèle.

En 1D, on utilisera la fonction interp1Documentation de la fonction interp1 qui propose les méthodes du plus proche voisin, linéaire, splines, cubique ainsi que l'extrapolation.

Pour des dimensions supérieures, on utilisera :

• sur des grilles régulières (générées habituellement avec les fonctions meshgridDocumentation de la fonction meshgrid et ngridDocumentation de la fonction ngrid), les fonctions interp2Documentation de la fonction interp2 (2D) et interp3Documentation de la fonction interp3 (3D) et interpnDocumentation de la fonction interpn (N-D, N≥1) ou la classe griddedInterpolantDocumentation de la classe griddedInterpolant (N-D, N≥1) ;
• sur des données non-ordonnées régulièrement, les fonctions griddataDocumentation de la fonction griddata (2D et 3D) griddatanDocumentation de la fonction griddatan (N-D, N≥2) ou la classe scatteredInterpolantDocumentation de la classe scatteredInterpolant (2D et 3D).

Numériquement, un système d'équations linéaires du style A.x = b pourra se résoudre à l'aide de l'opérateur \Documentation de l'opérateur \ (fonction mldivide) :

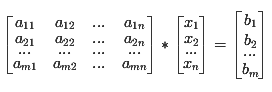
x = A\b;

Si l'on souhaite trouver le zéro d'une fonction continue, on pourra utiliser la fonction fzeroDocumentation de la fonction fzero.

La fonction fsolveDocumentation de la fonction fsolve de l'Optimization Toolbox sera utilisée pour résoudre des équations non-linéaires.

Ces deux fonctions seront utilisées sensiblement de la même manière :

x0 = … % point de départ

fun = @fonction_a_annuler;
% ou si l'on souhaite faire passer des arguments : 
fun = @(x) fonction_a_annuler(x, <entrées supplémentaires>);

x = fsolve(fun, x0); % idem fzero

avec séparément la définition de la fonction fonction_a_annuler :

function r = fonction_a_annuler(x, <éventuels arguments supplémentaires>)
r = …

Enfin, de façon formelle on pourra utiliser la fonction solveDocumentation de la fonction solve de la Symbolic Math Toolbox. Celle-ci pourra s'utiliser de deux façons.

Exemple pour l'équation  :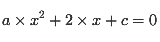

• avec des chaînes de caractères :

   

  Sélectionnez

  sol = solve('a*x^2 + 2*x + c', 'x') % résolution selon la variable x
  subs(sol, {'a','c'}, {1 1}) % Solution pour a=1 et c=1

• avec des variables symboliques :

   

  Sélectionnez

  syms a c x
  b = 2;
  sol = solve(a*x^2 + b*x + c, x)
  subs(sol, {a,c}, {1 1})

Numériquement, on utilisera les fonctions ode que l'on choisira à l'aide du premier tableau ODE Solvers.

Vous pourrez trouver un minitutoriel dans cette discussion ainsi qu'une astuce dans le second message permettant de résoudre des équations d'ordres supérieurs à un.

De manière formelle, la fonction dsolveDocumentation de la fonction dsolve de la Symbolic Math Toolbox qui pourra s'utiliser de deux façons :

• avec des chaînes de caractères, le « D » devant une variable signifiant « la dérivée de cette variable » :

   

  Sélectionnez

  dsolve('Dy == y + 1', 'x')

• avec des variables symboliques :

   

  Sélectionnez

  syms y(x)
  dsolve(diff(y) == y + 1, x)